Exponential dependence is a mathematical function that is useful for describing a process where the number of any elements rapidly increases or decreases rapidly. There are many examples of the use of this dependence in biology, physics, economics, medicine and other areas of human activity.
Exponential Determination
In order to understand what the words “this quantity grows exponentially” or “this process is characterized by an exponential decline” mean, it is necessary to consider the concept of the exponential function itself. To do this, take some positive number "a", which is not equal to 1, and raise it to the power of "x", while the variable x can have both positive and negative values, but it should not be zero. We also take some constant number k (constant), which is not equal to zero. Now we introduce the mathematical function f (x) = k * a x . Raising to the power "x" a positive number "a" is an exponential dependence, and the function f (x) itself is called exponential. In the function f (x), the number "a" is called the base, and "x" is an independent variable.
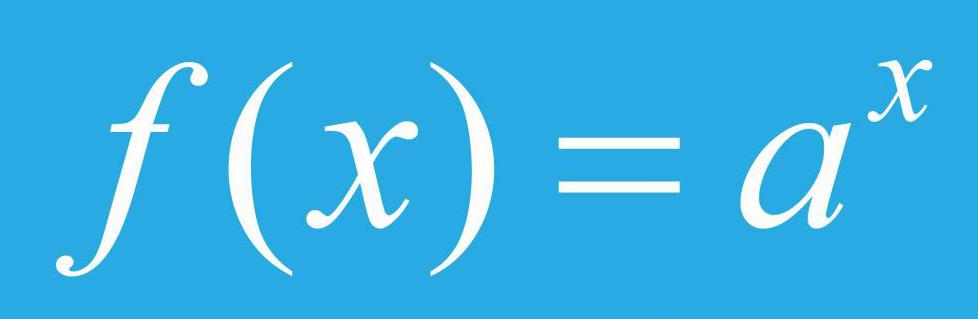
Note that in mathematics often appears the basis of the exponential function "a", which is approximately equal to 2.718. This number is denoted by the Latin letter "e" and is called the Euler number. The marked number plays an important role in the mathematical theory of limits, as well as in many physical processes in nature, for example, air pressure with altitude on our planet decreases exponentially, in the functional dependence of which the Euler number acts as the basis.
Exponential graph
Consider the properties of the exponential function y = a x , for this we turn to the graph presented above. The first important property is that no matter what the base “a” is, the function will always pass through the point with coordinates (0,1), since a 0 = 1.
It can also be seen from the graph of the exponential dependence that the function a x for any values of the variable "x" takes only positive values. For large negative values of "x" the function quickly approaches the abscissa axis, that is, tends to zero. In turn, even with small positive values of "x", the function increases sharply, while the rate of its increase also increases exponentially, which can be shown if we take the derivative of the function in question ((a x ) '= ln (a) * a x , where ln (a) is the natural logarithm).
Thus, the exponential dependence is a sharp change in a certain value both in the direction of its increase, and in the direction of decrease.
Chess story example
A good demonstration of the significance of the exponential increase in objects is an ancient legend associated with the invention of chess. According to this legend, for the entertainment of a Hindu king, whose name was Belkib, his close friend Brahman Sissa invented a chess board game for 3000 years BC.
The king was so happy about the new game that he promised to give Cissa everything he wanted. Then Brahman Sissa offered him to give as much grain as would fit on 64 chess squares, while on the 1st cell he put 1 grain, on the 2nd - 2 grains, on the 3rd - 4 grains and so on, doubling each time number. Belkib did not immediately understand how much he would need to give grain, so he accepted his friend’s offer without hesitation.
The number of grains that is placed on a chessboard according to the described principle will be 2 64 = 18 446 744 073 709 551 616 - a giant number!
Planet population growth
Another striking example of the processes that are described according to exponential dependence is the growth of the planet's population. So, in 1500, the planet’s population was about 500 million, in 1800, that is, 300 years later, it doubled and became equal to 1 billion, less than 50 years passed, and the planet’s population crossed the mark of 2 billion, currently the number of inhabitants on the planet Earth is 7.5 billion people.
Described by the example of humanity, population growth is characteristic of any biological species, whether it be a mammal or a unicellular bacterium. Mathematically, this growth is described by the following formula: N t = N 0 * e k * t , where N t and N 0 are the population at time t and zero, respectively, k is some positive coefficient. This mathematical model of population growth is called the exponential dependence in ecology.
The exponential growth of the planet's population made think at the beginning of the 19th century the famous English economist and demographer Thomas Robert Malthus. The scientist predicted in due time that in the middle of the 19th century hunger would come on Earth, as food production increases linearly, while the number of people on the planet increases exponentially. Malthus believed that the only way to achieve equilibrium in the system under consideration is mass mortality caused by wars, epidemics and other cataclysms.
As you know, the scientist made a mistake in his gloomy predictions, at least he made a mistake with the specified date.
Age of archaeological remains
Another striking example of natural processes that occur according to the exponential law is the decay of radioactive elements. This physical phenomenon, which consists in the conversion of nuclei of heavy elements into nuclei of lighter ones, is described by the following mathematical formula: N t = N 0 * e -k * t , where N t and N 0 are the number of nuclei of a heavier element at time t and at the initial moment, respectively. This formula shows that it is almost similar to that for the growth of the biological population, the only difference is the minus sign in the exponent, which indicates the loss of heavy nuclei.
The marked formula is used to determine the age of rocks and fossilized organisms. In the latter case, they work with the carbon isotope 14 C, since its half-life (the time during which the initial number of heavy nuclei is halved) is relatively small (5700 years).
Other processes subject to exponential law
Exponential dependence describes many processes in economics, chemistry, and medicine. For example, doses of drugs that enter the human body decrease exponentially in time. In the economy, investment profit, based on a certain initial capital, is also calculated according to the exponential law.