For a long time, people did not leave dreams of the interconversion of elements - more precisely, the transformation of various metals into one. After realizing the futility of these attempts, the point of view about the inviolability of chemical elements was established. And only the discovery of the structure of the nucleus at the beginning of the 20th century showed that the conversion of elements into one another is possible - but not by chemical methods, that is, by acting on the outer electronic shells of atoms, but by interfering with the structure of the atomic nucleus. Such phenomena (and some others) relate to nuclear reactions, examples of which will be discussed below. But first, it is necessary to recall some basic concepts that will be required during this consideration.
The general concept of nuclear reactions
There are phenomena in which the atomic nucleus of an element interacts with another nucleus or any elementary particle, that is, exchanges energy and momentum with them. Such processes are called nuclear reactions. Their result may be a change in the composition of the nucleus or the formation of new nuclei with the emission of certain particles. In this case, options such as:
- the conversion of one chemical element to another;
- nuclear fission ;
- synthesis, i.e. fusion of nuclei, in which the nucleus of a heavier element is formed.
The initial phase of the reaction, determined by the type and state of the particles entering it, is called the input channel. The output channels are the possible paths along which the reaction will proceed.
Rules for recording nuclear reactions
The examples below demonstrate the methods by which it is customary to describe reactions involving nuclei and elementary particles.
The first method is the same as that used in chemistry: the initial particles are placed on the left side, and the reaction products are placed on the right. For example, the interaction of the beryllium-9 nucleus with an incident alpha particle (the so-called neutron discovery reaction) is written as follows:
9 4 Be + 4 2 He → 12 6 C + 1 0 n.
The superscripts indicate the number of nucleons, that is, the mass numbers of nuclei, the subscripts indicate the number of protons, that is, atomic numbers. The sums of those and others in the left and right parts must match.
An abbreviated way of writing equations of nuclear reactions, often used in physics, is as follows:
9 4 Be (α, n) 12 6 C.
General view of such a record: A (a, b 1 b 2 ...) B. Here A is the target nucleus; a - incident particle or nucleus; b 1 , b 2 and so on are light reaction products; B is the final core.
Energy of nuclear reactions
In nuclear transformations, the law of conservation of energy is fulfilled (along with other conservation laws). In this case, the kinetic energy of particles in the input and output channels of the reaction can differ due to changes in the rest energy. Since the latter is equivalent to the mass of particles, the masses will also be different before and after the reaction. But the full energy of the system is always conserved.
The difference of the rest energy of the particles entering into the reaction and leaving it is called the energy output and is expressed in the change in their kinetic energy.
In processes involving nuclei, three types of fundamental interactions are involved - electromagnetic, weak and strong. Thanks to the latter, the core has such an important feature as high binding energy between its constituent particles. It is significantly higher than, for example, between a nucleus and atomic electrons or between atoms in molecules. This is evidenced by a noticeable mass defect - the difference between the sum of the nucleon masses and the mass of the nucleus, which is always less by an amount proportional to the binding energy: Δm = E cv / c 2 . The mass defect is calculated using the simple formula Δm = Zm p + Am n - M i , where Z is the nuclear charge, A is the mass number, m p is the mass of the proton (1.00728 amu), m n is the mass neutron (1.00866 amu), M i - mass of the nucleus.
In the description of nuclear reactions, the concept of specific binding energy is used (that is, per nucleon: Δmc 2 / A).
Link energy and core stability
The most stable, that is, the highest specific binding energy, are nuclei with a mass number from 50 to 90, for example, iron. This “peak of stability” is due to the off-center nature of nuclear forces. Since each nucleon interacts only with its neighbors, it is weaker bound on the surface of the nucleus than inside. The less interacting nucleons in the nucleus, the lower the binding energy, so the light nuclei are less stable. In turn, with an increase in the number of particles in the nucleus, the Coulomb repulsive forces between protons increase, so that the binding energy of heavy nuclei also decreases.
Thus, fusion reactions with the formation of a stable medium-mass nucleus are most probable, that is, energetically favorable, for light nuclei, while for heavy nuclei, on the contrary, decay and fission processes (often multi-stage), which also result in more stable products. These reactions are characterized by a positive and often very high energy yield, which accompanies an increase in the binding energy.
Below we consider some examples of nuclear reactions.
Decomposition reactions
Nuclei can undergo a spontaneous change in composition and structure, in which the emission of any elementary particles or fragments of the nucleus, such as alpha particles or heavier clusters.
So, with alpha decay, which is possible due to quantum tunneling, the alpha particle overcomes the potential barrier of nuclear forces and leaves the mother nucleus, which, accordingly, reduces the atomic number by 2, and the mass number by 4. For example, the radium-226 nucleus, emitting alpha particle converted to radon-222:
226 88 Ra → 222 86 Rn + α ( 4 2 He).
The decay energy of the radium-226 nucleus is about 4.87 MeV.
Beta decay due to weak interaction occurs without changing the number of nucleons (mass number), but with an increase or decrease in the nuclear charge by 1, when an antineutrino or neutrino is emitted, as well as an electron or positron. An example of a nuclear reaction of this type is beta-plus-decay of fluorine-18. Here, one of the protons of the nucleus turns into a neutron, the positron and neutrino are emitted, and fluorine turns into oxygen-18:
18 9 K → 18 8 Ar + e + + ν e .
The energy of beta decay of fluorine-18 is about 0.63 MeV.
Nuclear fission
Fission reactions have a much greater energy yield. This is the name of the process in which the core spontaneously or involuntarily breaks up into fragments of similar mass (usually two, rarely three) and some lighter products. A nucleus is divided if its potential energy exceeds the initial value by a certain amount, called the fission barrier. However, the probability of a spontaneous process even for heavy nuclei is small.
It increases significantly when the nucleus receives the corresponding energy from the outside (when a particle enters it). The neutron most easily penetrates into the nucleus, since it is not subject to electrostatic repulsion forces. The neutron hit leads to an increase in the internal energy of the nucleus, it is deformed with the formation of constriction and is divided. The fragments fly apart under the influence of Coulomb forces. An example of a nuclear fission reaction is demonstrated by uranium-235, which has absorbed a neutron:
235 92 U + 1 0 n → 144 56 Ba + 89 36 Kr + 3 1 0 n.
The fission of barium-144 and krypton-89 is only one of the possible options for the division of uranium-235. This reaction can be written in the form 235 92 U + 1 0 n → 236 92 U * → 144 56 Ba + 89 36 Kr + 3 1 0 n, where 236 92 U * is a highly excited compound nucleus with high potential energy. Its excess, along with the difference in the binding energies of the parent and daughter nuclei, is released mainly (about 80%) in the form of the kinetic energy of the reaction products, and also partially in the form of the potential energy of fission fragments. The total fission energy of a massive nucleus is approximately 200 MeV. In terms of 1 gram of uranium-235 (provided that all nuclei have reacted), this amounts to 8.2 ∙ 10 4 megajoules.
Chain reactions
The fission of uranium-235, as well as nuclei such as uranium-233 and plutonium-239, is characterized by one important feature - the presence of free neutrons among the reaction products. These particles, penetrating into other nuclei, in turn, are able to initiate their fission again with the release of new neutrons and so on. A similar process is called a nuclear chain reaction.
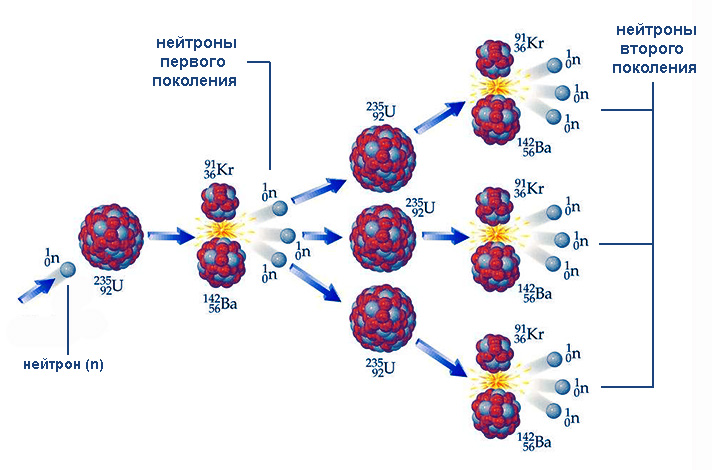
The course of the chain reaction depends on how the number of emitted neutrons of the next generation is related to the number of them in the previous generation. This ratio k = N i / N i –1 (here N is the number of particles, i is the generation number) is called the neutron multiplication coefficient. For k <1, the chain reaction does not occur. For k> 1, the number of neutrons, and hence the fissile nuclei, increases in an avalanche-like manner. An example of a chain nuclear reaction of this type is the explosion of an atomic bomb. At k = 1, the process proceeds stationary, an example of which is a reaction controlled by neutron-absorbing rods in nuclear reactors.
Nuclear fusion
The greatest energy release (per nucleon) occurs during the fusion of light nuclei - the so-called fusion reactions. To enter into a reaction, positively charged nuclei must overcome the Coulomb barrier and approach a strong interaction distance not exceeding the size of the nucleus itself. Therefore, they must have extremely high kinetic energy, which means high temperatures (tens of millions of degrees and above). For this reason, fusion reactions are also called thermonuclear.
An example of a nuclear fusion reaction is the formation of helium-4 with neutron emission during the fusion of the deuterium and tritium nuclei:
2 1 H + 3 1 H → 4 2 He + 1 0 n.
An energy of 17.6 MeV is released here, which, per nucleon, is more than 3 times higher than the fission energy of uranium. Of these, 14.1 MeV falls on the kinetic energy of the neutron and 3.5 MeV - helium-4 nuclei. This significant value is created due to the huge difference in the binding energies of the nuclei of deuterium (2.2246 MeV) and tritium (8.4819 MeV) on the one hand, and helium-4 (28.2956 MeV) on the other.
In fission reactions, the energy of electrical repulsion is released, while in the synthesis, energy is released due to the strong interaction - the most powerful in nature. This determines such a significant energy yield of this type of nuclear reaction.
Examples of solving problems
Consider the fission reaction 235 92 U + 1 0 n → 140 54 Xe + 94 38 Sr + 2 1 0 n. What is its energy output? In general terms, the formula for its calculation, which reflects the difference in the rest energies of particles before and after the reaction, is as follows:
Q = Δmc 2 = (m A + m B - m X - m Y + ...) ∙ c 2 .
Instead of multiplying the speed of light by the square, you can multiply the mass difference by a factor of 931.5 and get the energy value in megaelectron-volts. Substituting the corresponding values of atomic masses in the formula, we obtain:
Q = (235.04393 + 1.00866 - 139.92164 - 93.91536 - 2 ∙ 1.00866) ∙ 931.5 ≈ 184.7 MeV.
Another example is the synthesis reaction. This is one of the stages of the proton-proton cycle - the main source of solar energy.
3 2 He + 3 2 He → 4 2 He + 2 1 1 H + γ.
Apply the same formula:
Q = (2 ∙ 3.01603 - 4.00260 - 2 ∙ 1.00728) ∙ 931.5 ≈ 13.9 MeV.
The main share of this energy - 12.8 MeV - falls in this case on a gamma photon.
We considered only the simplest examples of nuclear reactions. The physics of these processes is extremely complex, they are very diverse. The study and application of nuclear reactions is of great importance both in the practical field (energy) and in fundamental science.