One of the basic physical principles of the interaction of solids is the law of inertia, formulated by the great Isaac Newton. We come across this concept almost constantly, since it has an extremely large impact on all the material objects of our world, including man. In turn, such a physical quantity as the moment of inertia is inextricably linked with the law mentioned above, determining the strength and duration of its effect on solids.
From the point of view of mechanics, any material object can be described as an invariable and clearly structured (idealized) system of points, the mutual distances between which do not change depending on the nature of their movement. This approach allows you to accurately calculate by special formulas the moment of inertia of almost all solids. Another interesting nuance here is that any complex movement that has the most intricate trajectory can be represented as a combination of simple movements in space: rotational and translational. This also makes life easier for physicists in calculating a given physical quantity.
To understand what exactly is the moment of inertia and what is its effect on the world around us, the easiest way is by the example of a sharp change in the speed of a passenger vehicle (braking). In this case, the legs of a standing passenger friction on the floor will carry away. But at the same time, no effect will be exerted on the body and head, as a result of which they will continue to move for some time at the same predetermined speed. As a result, the passenger will lean forward or fall. In other words, the moment of inertia of the legs, extinguished by the force of friction on the floor, will be significantly less than the other points of the body. The opposite picture will be observed with a sharp increase in the speed of the bus or tram car.
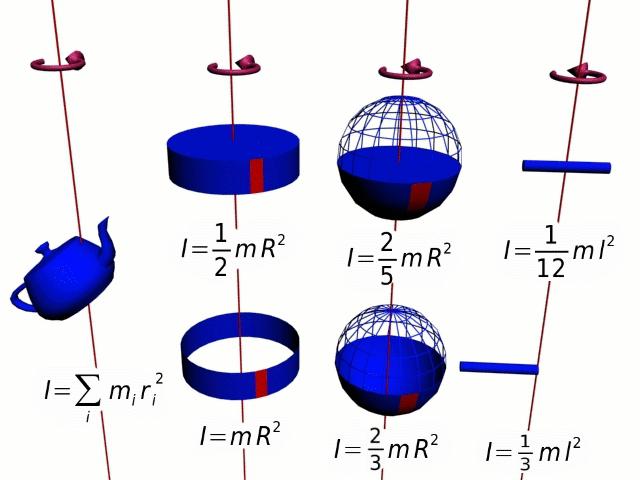
The moment of inertia can be formulated as a physical quantity equal to the sum of the products of elementary masses (those same individual points of a solid) by the square of their distance from the axis of rotation. From this definition it follows that this characteristic is an additive quantity. Simply put, the moment of inertia of a material body is equal to the sum of similar indicators of its parts: J = J 1 + J 2 + J 3 + ...
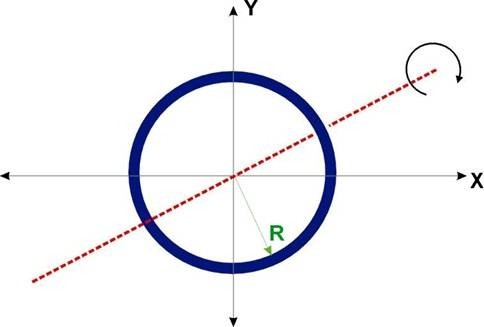
This indicator for bodies of complex geometry is found experimentally. One has to take into account too many different physical parameters, including the density of the object, which can be inhomogeneous at different points, which creates the so-called mass difference in different segments of the body. Accordingly, the standard formulas are not suitable here. For example, the moment of inertia of a ring with a certain radius and uniform density, having an axis of rotation that passes through its center, can be calculated by the following formula: J = mR
2 . But in this way it will not work to calculate this value for a hoop, all parts of which are made of different materials.
And the moment of inertia of the ball of a continuous and homogeneous structure can be calculated by the formula: J = 2 / 5mR 2 . When calculating this indicator for bodies relative to two parallel rotation axes, an additional parameter is introduced into the formula — the distance between the axes, denoted by the letter a. The second axis of rotation is indicated by the letter L. For example, the formula may have the following form: J = L + ma 2 .
Thorough experiments on the inertial motion of bodies and the nature of their interaction were first made by Galileo Galilei at the junction of the sixteenth and seventeenth centuries. They allowed the great scientist, ahead of his time, to establish the basic law on the preservation by physical bodies of a state of rest or rectilinear motion relative to the Earth in the absence of exposure to other bodies. The law of inertia was the first step in establishing the basic physical principles of mechanics, while still completely vague, slurred and obscure. Subsequently, Newton, formulating the general laws of motion of bodies, included the law of inertia in their number.