The Gauss theorem is one of the fundamental laws of electrodynamics, structurally included in the system of equations of another great scientist - Maxwell. It expresses the relationship between the intensity flows of both electrostatic and electrodynamic fields passing through a closed type surface. The name of Carl Gauss sounds no less loud in the scientific world than, for example, Archimedes, Newton or Lomonosov. In physics, astronomy, and mathematics, there are not so many fields that the brilliant German scientist did not directly contribute to the development of.
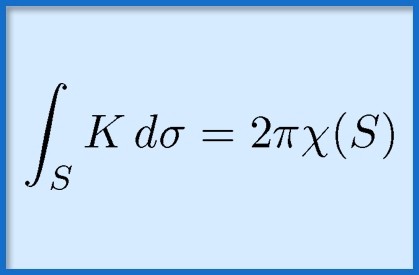
The Gauss theorem played a key role in the study and understanding of the nature of electromagnetism. By and large, it became a kind of generalization and, to some extent, an interpretation of the famous Coulomb law. This is just the case, not so rare in science, when the same phenomena can be described and formulated in different ways. But the Gauss theorem not only acquired applied value and practical application, it helped to look at the well-known laws of nature from a slightly different angle.
In a way, she contributed to a grand breakthrough in science, laying the foundation for modern knowledge in the field of electromagnetism. So what is the Gauss theorem and what is its practical application? If we take a pair of static point charges, then the particle brought to them will be attracted or repelled with a force that is equal to the algebraic sum of the values of all elements of the system. Moreover, the intensity of the total aggregate field formed as a result of such an interaction will be the sum of its individual components. This ratio is widely known as the principle of superposition, which allows to accurately describe any system created by multivector charges, regardless of their total number.
However, when there are a lot of such particles, scientists initially had certain difficulties in the calculations that could not be resolved by applying the Coulomb law. The Gauss theorem for the magnetic field helped to overcome them, which, however, is valid for any force systems of charges having a decreasing strength proportional to r −2 . Its essence boils down to the fact that an arbitrary number of charges surrounded by a closed surface will have a total flow of tension equal to the total value of the electric potential of each point of this plane. Moreover, the principles of interaction between elements are not taken into account, which greatly simplifies the calculation. Thus, this theorem allows us to calculate the field even with an infinite number of charge carriers.

True, in reality this is possible only in some cases of their symmetrical arrangement, when there is a convenient surface through which the strength and intensity of the flow are easily calculated. For example, a test charge placed inside a conducting body of a spherical shape will not experience the slightest force impact, since the field strength index there is zero. The ability of conductors to push out various electric fields from themselves is explained solely by the presence of charge carriers in them. In metals, this function is performed by electrons. Such features are today widely used in technology to create various spatial areas in which electric fields do not act. These phenomena are perfectly explained by the Gauss theorem for dielectrics, whose influence on systems of elementary particles reduces to the polarization of their charges.
To create such effects, it is enough to surround a certain area of tension with a metal shielding grid. This protects sensitive electric devices and people from the effects of electric fields.