The mathematical program MathCAD is used in complex algebraic calculations at a time when they are difficult or impossible manually. This resource greatly facilitates the life of many technical, economic specialties and students. It is very simple to simulate a problem in a mathematical form and get the desired answer. However, the interface may be incomprehensible to beginners, and it is difficult for them to adequately perceive this computing environment. One of the stumbling blocks is how to solve the system of equations in Matkad. This is a very important function that should be studied by anyone who wishes to continue to work in this program.
How to solve the system of equations in Matkada
Actually, this is not the simplest task, but you can learn how to solve them using the examples considered. Very often, users are faced with systems of equations and the concept of "parameter". In a mathematical working environment, the parameter and how to solve the system of equations in the Matkada is found using the auxiliary function root. Besides the fact that we have to involve this function in the solution, we also need the value of the initial approximation. In general, there are several types of systems of equations, therefore, we will consider specifically on different types. We will discuss what problems the user may encounter when using the root function.
- The equation in its original form has no roots.
- The roots of the equation are at a fairly far distance from the initial approximation.
- The equation undergoes a gap between the initial approximation and the roots.
- The equation has a maximum and a minimum between the initial approximation and the roots.
- The equation has a complex root, provided that the initial approximation was real.
Complex function and its schedule
Let's start with the simplest and most distant topic, to gradually introduce new users to the course. This is necessary in order to symbolically solve the Matkad equation system, but first we’ll try to build a graph for a complex function. The user needs to bring the wording in mathematical form so that the function graph is built correctly - since we have three sections, it makes sense to use the software design. To carry out the correct writing of the equation, we use the if-otherwise block.
To solve the system of linear equations in Matkada, you can use some other options. The first way is that we write our system of equations through the if statement. In the second method, it is necessary to resort to the method of logical factors.
We build a quick chart by pressing the key combination Shift + 2. In the chart window that appears, enter the function in the middle vertical block and in the lower vertical block - the argument "x".
System of nonlinear equations
For a non-linear equation, the order of finding the roots is not much different from another type. Suppose we have a function f (x) = (e ^ x / (2 (x-1) ^ 2) -10 in the range from -10 to 10. In order to solve the system of nonlinear equations in Matkada, you need to build graph to evaluate zeros and use tabs.
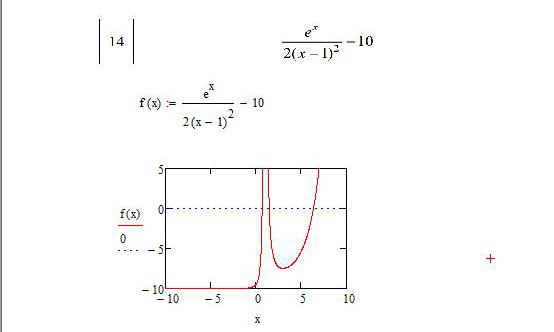
- We set this function in mathematical form, which can be processed by the computing environment.
- We plot the function with the keys Shift + 2, denoting the function in the vertical middle window. In the horizontal we set the boundaries, as in the interval: from -10 to 10, and enter the argument "x" in the middle cell.
- Now we need to visually indicate the zeros on the chart. This can be done by adding the function 0 (it is entered into the middle vertical cell using the "," symbol). It has become visually clearer where the zeros of the function are located.
- It’s time to tabulate the graph, but you need to specify a range of values. In the case under consideration, we will have x: = - 1, 0.5 .. 7 (the colon sign is placed using the ";" key. Now we will track the sign change by evaluating the values of f (x).
Finding roots using the root function
Before solving the system of equations in Matkad, you must perform the root operation. Previously it was necessary to build a function and tabulate it. After all operations, you can begin to search for roots with a given interval. So, using the example of a nonlinear equation, we will answer the question of how to solve the system of equations in Matkad:
- You must find the first root of the "root" function. Assign the following command to "x": x 1 : = root (f (x), x, -10,10). Then we print the value of the argument "x" and the function f (x 1 ).
- Find the second root using the same function. The only difference will be that the root search will go through the initial approximation task. Take the initial approximation "x: = 0" to apply root without an interval. We set the function: x 2 = root (f (x), x), and then we find the value of the argument and its function in the same way as in the previous example.
Find roots with find
Unlike the previous function, the interval or initial approximation is not used here. This command works by assigning an initial condition - near the root. We will analyze the operation of this function using the same example:
- It is necessary to indicate the initial condition: x: = 7.
- We use the Given case for our function and assign "thick equal" to f (x) = 0.
- Now we use the function itself: x 3 : = find (x).
- We search for the value of the argument and its function.